Definizione
Un albero consiste di un insieme di nodi e un insieme di archi orientati che connettono coppie di nodi, con le seguenti proprietà:
- Un nodo dell’albero è designato come nodo radice;
- Ogni nodo
, a parte la radice, ha esattamente un arco entrante; - Esiste un cammino unico dalla radice ad ogni nodo;
- L’albero è connesso.
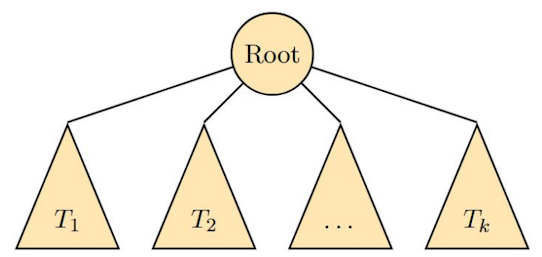
Un albero è dato da un insieme vuoto oppure un nodo radice e zero o più sottoalberi, ognuno dei quali è un albero; la radice è connessa alla radice di ogni sottoalbero con un arco orientato.
Terminologia
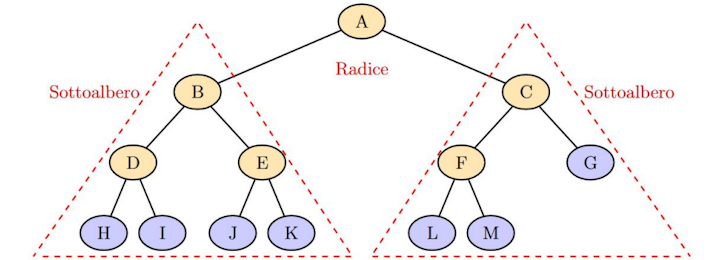
| Elemento | Definizione |
|---|---|
| Radice | |
| Padre di | |
| Radici dei sottoalberi | |
| Fratelli, figli di | |
| Nodi viola | Foglie |
| Altri nodi | Nodi interni |
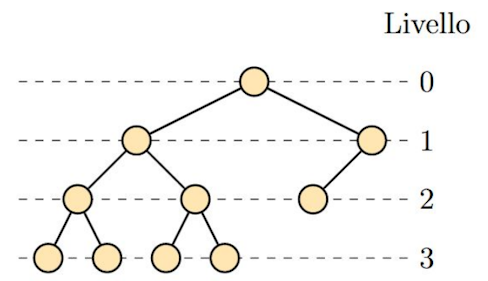
| Elemento | Definizione |
|---|---|
| Profondità dei nodi (depth) | Lunghezza del cammino semplice dalla radice al nodo, misurato in numero di archi. |
| Livello (level) | Insieme di nodi alla stessa profondità. |
| Altezza dell’albero (height) | Profondità massima delle foglie. |
Memorizzazione
Esistono diversi modi per memorizzare un albero a seconda del numero massimo e medio di figli presenti:
- Realizzazione primo figlio, prossimo fratello se ogni nodo può avere un numero arbitrario di figli;
- Realizzazione con vettore dei figli se si sa mediamente quanti figli ci sono per ogni nodo, che avrà un riferimento al nodo padre;
- Realizzazione con vettore dei padri se interessa mantenere solo la relazione figlio → padre.
Tipi di alberi
Albero binario
Un albero binario è un albero radicato in cui ogni nodo ha al massimo due figli, identificati come figlio sinistro e figlio destro. Ogni nodo ha un riferimento al nodo padre e ai due figli.
Albero generico
Un albero generico è un albero radicato in cui ogni nodo ha un numero arbitrario di figli, o nessuno.
Visita di un albero
Una visita è una strategia per analizzare (visitare) tutti i nodi di un albero, ossia scansionarne tutti i valori.
Visita in profondità (DFS - Depth First Search)
Per visitare un albero, si visita ricorsivamente ognuno dei suoi sottoalberi; richiede uno stack di appoggio ed ha tre varianti: pre/in/post visita (pre/in/post order).



Visita in ampiezza (BFS - Breadth-First Search)
Ogni livello dell’albero viene visitato uno dopo l’altro; richiede una coda.

Costo computazionale delle visite
Dato che ogni nodo viene visitato al massimo una volta (se l’algoritmo è implementato correttamente), il costo di una visita di un albero contenente